英語で書かれた海外の中学数学にふれていただくことを通して、英語の学習、習得を支援します。
ページ下部に、関数と座標平面上のグラフの関連で身に着けたい英単語を厳選してあります。
日々の数学の学習時などに繰り返し思い出してください。確実に語彙力が上がります。
数学用語と解説
関係
- An ordered pair is two numbers or letters (or anything else) written in the form (x, y).
順序対とは (x, y) の形式で書かれたふたつの数字または文字(またはその他何でも)のこと。 - A relation is a set of ordered pairs.
関係とは順序対の集合のこと。 - The domain is the set of all the first elements (or x-values) of each ordered pair.
変域とはそれぞれの順序対の1番目の要素(xの値)全ての集合のこと。 - The range is the set of all the second elements (or y-values) of each ordered pair.
値域とはそれぞれの順序対の2番目の要素(yの値)全ての集合のこと。

Relations
関数
- A relation is a function if there is exactly one y-value for each x-value.
それぞれのxの値についてちょうどひとつのyの値があるならば、その関係は関数である。 - You can think of a function as an input-output machine.
関数は入出力の機械と考えることができる。
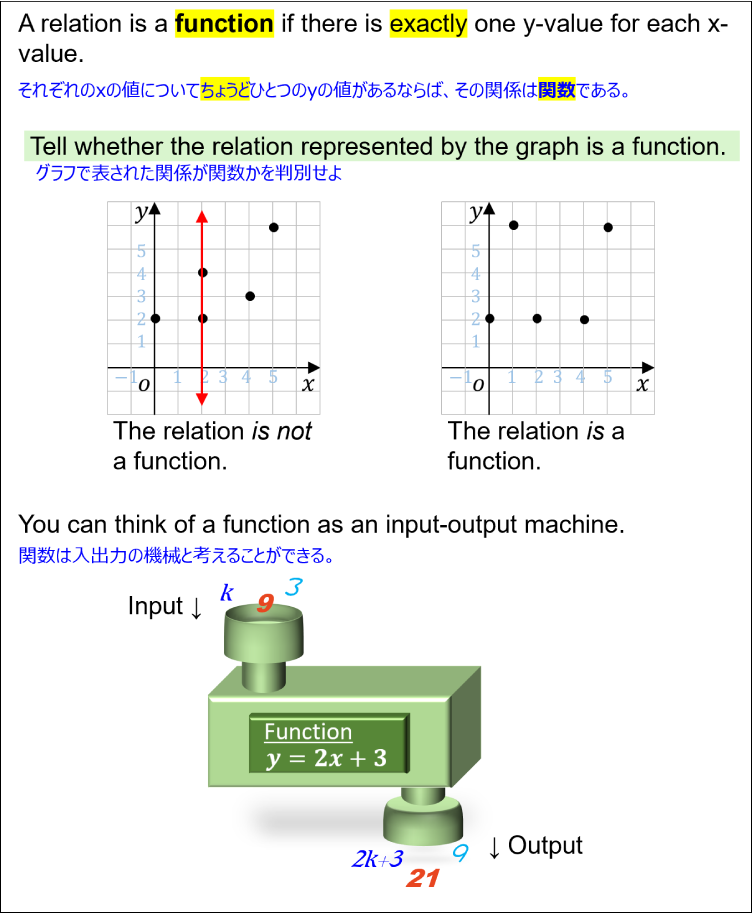
Functions
座標平面
- A coordinate plane is formed by a horizontal and vertical number line, called coordinate axes.
座標平面は水平と垂直の数直線(座標軸とよぶ)で形成される。 - The horizontal axis is the x-axis.
水平の軸はx軸。 - The vertical axis is the y-axis.
垂直の軸はy軸。 - The axes meet at a point called the origin.
ふたつの軸は原点とよぶ点で交わる。
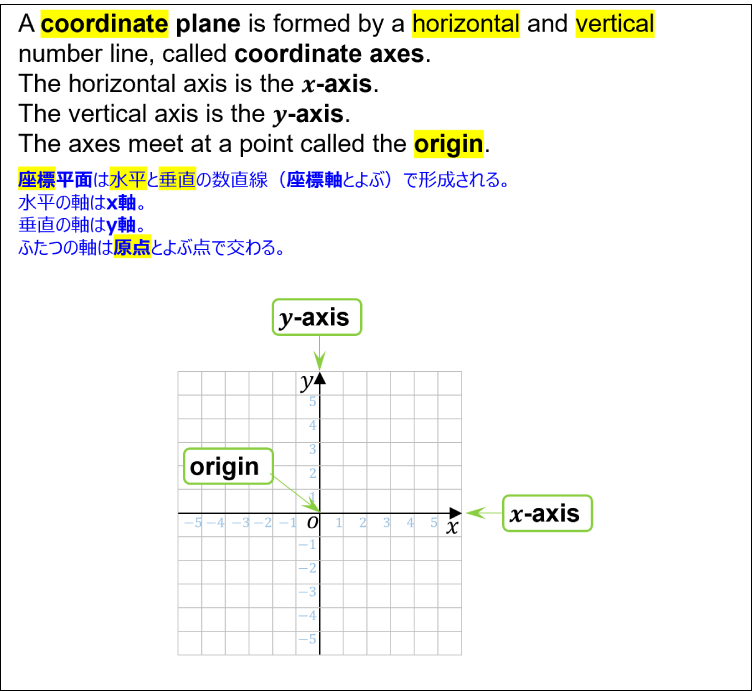
Coordinate Plane
座標平面上の点
- Each point in a coordinate plane is represented by an ordered pair (x, y).
座標平面上の各点は順序対(x,y)で表される。 - The first number is the x-coordinate, and the second number is the y-coordinate.
1番目の数をx座標、2番目の数をy座標とよぶ。 - The coordinates are written as (x, y).
座標は(x,y)と書く。

Graphing Points in a Coordinate Plane
WORDS AND PHRASES
✅relate 関係がある
/relate A to B: AをBと関係づける
📎relation {複数の物の間の}関係
✅domain {扱う}領域、分野
✅range 範囲
✅exact 正確な 📎exactly 正確に
✅function 機能;関数
/機能する
✅coordinate {うまく行くよう活動など}を調整する;{服など}を合わせる
/座標
/重要度が同じな ⇔📎subordinate 下位の
✅origin 起源
✅vertical 垂直な ⇔📎horizontal 水平な
✅represent を代表する;に相当する;を表す
TIPS
座標とcoordinate
coordinateは「調整する」と「座標」の両方を覚えましょう。
ちなみに「座標」をcoordinateとよぶのは、xとyがうまく調整・アレンジされているから、というわけではありません。
xとyが同じ重要度だからです。
coordinateの形容詞の意味と同じ。
詳細は以下の通りです。
coordinateとよぶ経緯、意味:
「ライプニッツが1694年に厳密に現代の意味での”coordinate”という言葉を最初に使い、ふたつのordinatesを同じ条件で認識した。」(*1)
ふたつのordinatesとは、図形問題で使われていたある種の補助線 ”abscissa”と“ordinate”(*2)のこと。
現代の意味とは、「ふたつが同じ強さであり、共同でひとつの点などを表現する」(*3)ということ。
”coordinate “のcoはcoauthor共同執筆者、cofounder共同創業者のように「共同」の意味。
*1:Boyer, Barl B (2004 ). History of Analytic Geometry. Dover Publications, Inc: Mineola, New York. p133
*2:abscissa:切断された直線の意 訳は「横線」 x座標のもとになった用語
ordinate: 平行線の意 訳は「縦線」 y座標のもとになった用語
*3:Sofia Neovius (2013). René Descartes’ Foundations of Analytic Geometry and Classification of Curves p20
その他
Mapping Diagramは適切な日本語が調べても見当たりませんでした。
ここでのmappingは写像でないケース(例示のような)も含むので、勝手ながら「対応図」と記載しておきました。
値域は日本では高校まで出てきません。
中3でも「yの変域」という言葉です。


