STEM-Plus Content offers K-12 math and other STEM content in both English and Japanese.
The content aids in vocabulary acquisition for both English and Japanese learners.
How does it achieve this?
Through the content, learners grasp words and phrases more intuitively because they already know their meanings in their native language.
It is like learning the word “apple” by looking at a picture of one.
STEM-Plus Content facilitates easy learning of abstract yet useful words.
To ensure effective and efficient learning, the content is designed to be concise and illustrative.
Learners can easily understand the material through images and examples.
In addition, the content provides useful tips on math and other STEM subjects, supporting
academic success in these important fields.
How to use:
Carefully selected English words and phrases related to “Functions and Graphs on the Coordinated Planes” are highlighted in yellow in the images below. The words are also summarized at the bottom of this page.
We recommend reviewing them regularly during your daily math studies to enhance your vocabulary.
TERMS, DEFINITIONS, AND ILLUSTRATIONS
Relations
- An ordered pair is two numbers or letters (or anything else) written in the form (x, y).
順序対とは (x, y) の形式で書かれたふたつの数字または文字(またはその他何でも)のこと。 - A relation is a set of ordered pairs.
関係とは順序対の集合のこと。 - The domain is the set of all the first elements (or x-values) of each ordered pair.
変域とはそれぞれの順序対の1番目の要素(xの値)全ての集合のこと。 - The range is the set of all the second elements (or y-values) of each ordered pair.
値域とはそれぞれの順序対の2番目の要素(yの値)全ての集合のこと。

Relations
Functions
- A relation is a function if there is exactly one y-value for each x-value.
それぞれのxの値についてちょうどひとつのyの値があるならば、その関係は関数である。 - You can think of a function as an input-output machine.
関数は入出力の機械と考えることができる。
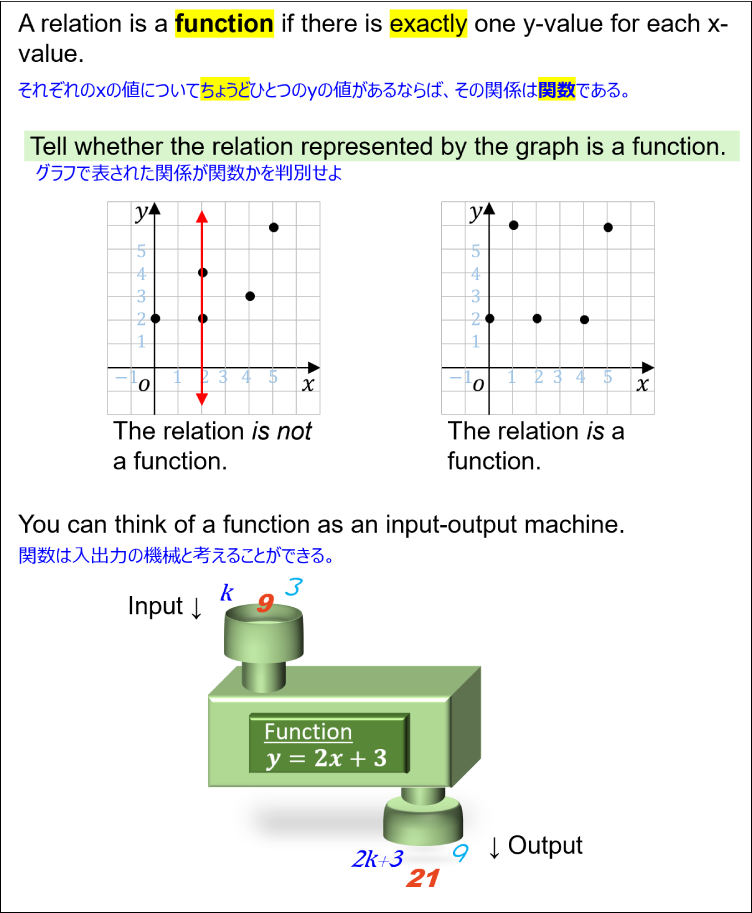
Functions
Coordinate Planes
- A coordinate plane is formed by a horizontal and vertical number line, called coordinate axes.
座標平面は水平と垂直の数直線(座標軸とよぶ)で形成される。 - The horizontal axis is the x-axis.
水平の軸はx軸。 - The vertical axis is the y-axis.
垂直の軸はy軸。 - The axes meet at a point called the origin.
ふたつの軸は原点とよぶ点で交わる。
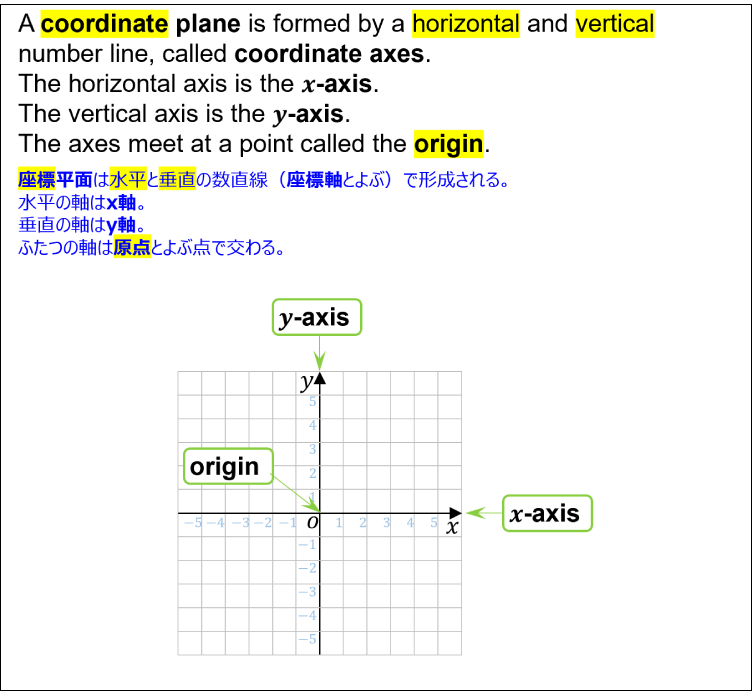
Coordinate Plane
Points in a Coordinate Plane
- Each point in a coordinate plane is represented by an ordered pair (x, y).
座標平面上の各点は順序対(x,y)で表される。 - The first number is the x-coordinate, and the second number is the y-coordinate.
1番目の数をx座標、2番目の数をy座標とよぶ。 - The coordinates are written as (x, y).
座標は(x,y)と書く。

Graphing Points in a Coordinate Plane
WORDS AND PHRASES
✅relate 関係がある
/relate A to B: AをBと関係づける
📎relation {複数の物の間の}関係
✅domain {扱う}領域、分野
✅range 範囲
✅exact 正確な 📎exactly 正確に
✅function 機能;関数
/機能する
✅coordinate {うまく行くよう活動など}を調整する;{服など}を合わせる
/座標
/重要度が同じな ⇔📎subordinate 下位の
✅origin 起源
✅vertical 垂直な ⇔📎horizontal 水平な
✅represent を代表する;に相当する;を表す
TIPS
“Coordinate (Planes)”とcoordinate
Please remember that “coordinate” can mean both “adjust” and “Coordinate (Plane).”
By the way, the reason we use “coordinate” to refer to “Coordinate (Planes)” is not because x and y are arranged or adjusted well. It’s because x and y have the same level of importance, which is the same as the adjective meaning of “coordinate.” Here are the details:
Origin and meaning of “Coordinate (Planes)”
“Leibniz in letters of 1694 first used the word “coordinates” in the strictly modern sense and recognized the two coordinates as on the same footing.” (*1)
The two coordinates refer to a certain type of auxiliary line “abscissa” and “ordinate”(*2) used in geometry problems.
The modern sense means that “both coordinates are equally strong and together describe a point in the plane or space.”(*3)
So, the “co” in “Coordinate (Planes)” means “joint” as in coauthor and cofounder.
*1:Boyer, Barl B (2004 ). History of Analytic Geometry. Dover Publications, Inc: Mineola, New York. p133
*2: Abscissa means “horizontal line” and refers to a cut line, which became the basis of x-coordinates.
Ordinate means “vertical line” and refers to a parallel line, which became the basis of y-coordinates.
*3:Sofia Neovius (2013). René Descartes’ Foundations of Analytic Geometry and Classification of Curves p20
Other tips
We couldn’t find an appropriate Japanese translation for “mapping diagram.”
Since “mapping” can refer to cases other than “写像” (like we have shown in the above example), we have arbitrarily used “対応図” to describe it.
In Japan, “the range” is not introduced until high school. Even in the third year of junior high school, we use the term “the domain of y-values” instead.



