STEM-Plus Content offers K-12 math and other STEM content in both English and Japanese.
The content aids in vocabulary acquisition for both English and Japanese learners.
How does it achieve this?
Through the content, learners grasp words and phrases more intuitively because they already know their meanings in their native language.
It is like learning the word “apple” by looking at a picture of one.
STEM-Plus Content facilitates easy learning of abstract yet useful words.
To ensure effective and efficient learning, the content is designed to be concise and illustrative.
Learners can easily understand the material through images and examples.
In addition, the content provides useful tips on math and other STEM subjects, supporting
academic success in these important fields.
How to use:
Carefully selected English words and phrases related to “Proportionality” are highlighted in yellow in the images below. The words are also summarized at the bottom of this page.
We recommend reviewing them regularly during your daily math studies to enhance your vocabulary.
TERMS, DEFINITIONS, AND ILLUSTRATIONS
Direct Proportionality
- Two quantities x and y are directly proportional when y=kx, where k is a nonzero constant.
y=kx でkがゼロでない定数のとき、ふたつの量xとyは比例するという。 - The number k is called the constant of proportionality.
kを比例定数とよぶ。 - The ratio y/x is constant and equal to k.
比 y/x は一定で比例定数kに等しい。 - The graph of y=kx is a line that passes through the origin.
y=kx のグラフは原点を通る直線である。
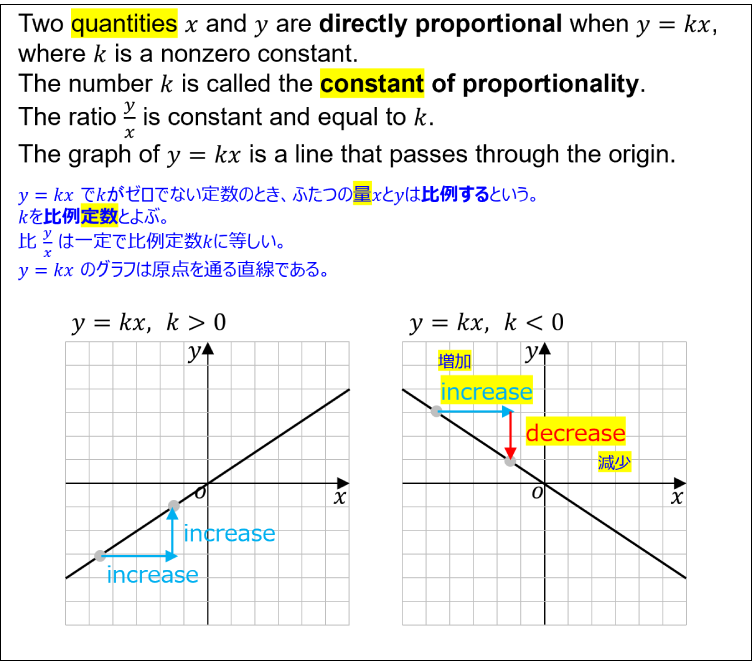
Illustration of directly Proportional Functions
Inverse Proportionality
- Two quantities x and y are inversely proportional when y=k/x, where k is a nonzero constant.
y=k/x でkがゼロでない定数のとき、ふたつの量xとyは反比例するという。 - The number k is called the constant of proportionality.
kを比例定数とよぶ。 - The product xy is constant and equal to k.
積 xy は一定で比例定数kに等しい。 - The graph of y=k/x is a hyperbola.
y=k/x のグラフは双曲線である。
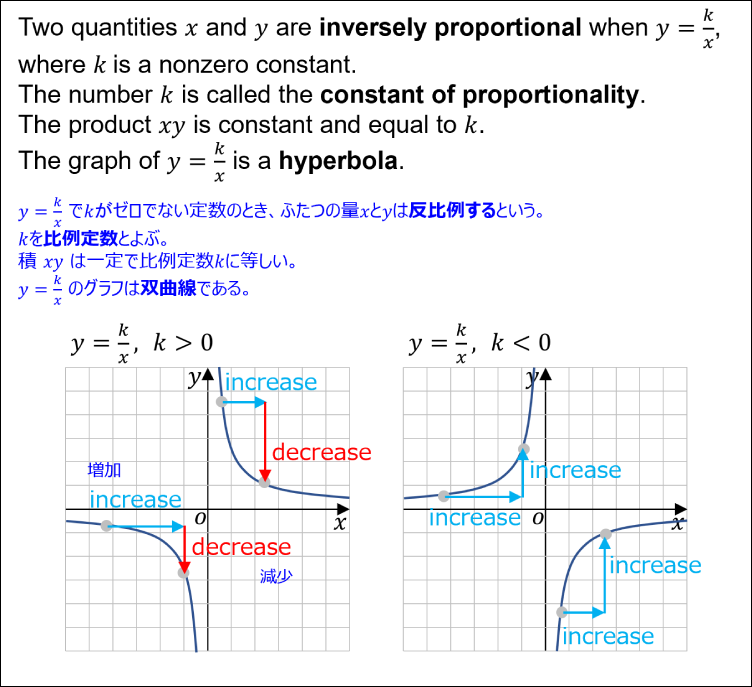
Illustration of Inversely Proportional Functions
WORDS AND PHRASES
✅quantity 量 ⇔quality 質
✅constant 一定の
✅increase 増加する;を増やす/増加
✅decrease 減少する;を減らす/減少
TIPS
Increasing Functions and Positive Slopes
When ‘x increases’ → How ‘y behaves’
↑ ↑
Developing the habit of fixing your attention here (‘x increases’) will bring various benefits in the future.
Specifically,
- terms like ‘increasing’ and ‘decreasing’ functions,
- expressions like a function is ‘increasing’ or ‘decreasing’ in a certain interval,
- and determining whether the slope is ‘positive’ or ‘negative’ as another way to say the above,
all refer to the ‘increase’ or ‘decrease’ of y when ‘x increases’.
It’s good to get accustomed to this early on.
About Inverse Proportionality
Inverse proportionality is indeed difficult.
As we all know, x cannot be zero.
But it’s hard to intuitively understand the behavior of y before and after this point.
As x approaches zero, like at -0.1, -0.01, y becomes a large negative number, like -10, -100,
and as x gets even closer to zero, y also becomes a larger negative number (eventually approaching negative infinity).
Then, the moment x exceeds zero by even a little, y jumps to positive infinity.
It’s baffling.
And not to mention, drawing its graph requires skill!
In some English-speaking countries, inverse proportionality is often introduced much later as a rational function.
Specifically, after studying quadratic, cubic, n-th degree functions, and even exponential and logarithmic functions.
However, it’s a relationship we often encounter in daily life.
So Don’t be too averse to it. Instead, let’s just recognize that it’s like a character shrouded in mystery.



